19. Summary
Summary
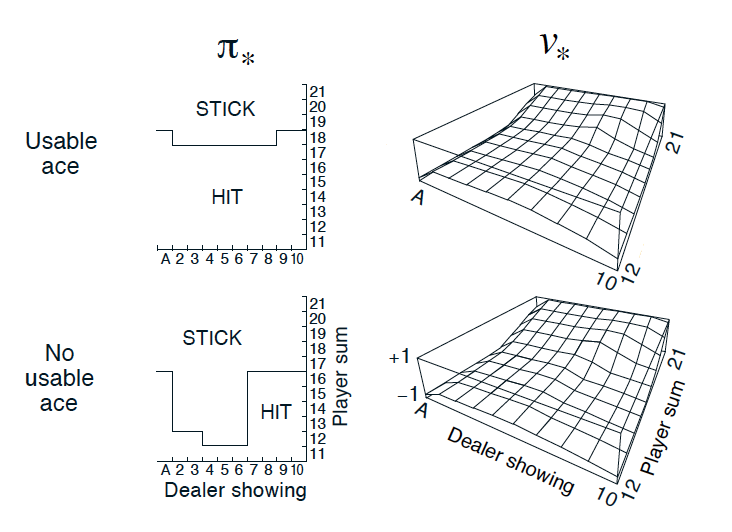
Optimal Policy and State-Value Function in Blackjack (Sutton and Barto, 2017)
### Monte Carlo Methods
- Monte Carlo methods - even though the underlying problem involves a great degree of randomness, we can infer useful information that we can trust just by collecting a lot of samples.
- The equiprobable random policy is the stochastic policy where - from each state - the agent randomly selects from the set of available actions, and each action is selected with equal probability.
### MC Prediction
- Algorithms that solve the prediction problem determine the value function v_\pi (or q_\pi ) corresponding to a policy \pi .
- When working with finite MDPs, we can estimate the action-value function q_\pi corresponding to a policy \pi in a table known as a Q-table . This table has one row for each state and one column for each action. The entry in the s -th row and a -th column contains the agent's estimate for expected return that is likely to follow, if the agent starts in state s , selects action a , and then henceforth follows the policy \pi .
- Each occurrence of the state-action pair s,a ( s\in\mathcal{S},a\in\mathcal{A} ) in an episode is called a visit to s,a .
-
There are two types of MC prediction methods (for estimating
q_\pi
):
- First-visit MC estimates q_\pi(s,a) as the average of the returns following only first visits to s,a (that is, it ignores returns that are associated to later visits).
- Every-visit MC estimates q_\pi(s,a) as the average of the returns following all visits to s,a .
### Greedy Policies
- A policy is greedy with respect to an action-value function estimate Q if for every state s\in\mathcal{S} , it is guaranteed to select an action a\in\mathcal{A}(s) such that a = \arg\max_{a\in\mathcal{A}(s)}Q(s,a) . (It is common to refer to the selected action as the greedy action .)
- In the case of a finite MDP, the action-value function estimate is represented in a Q-table. Then, to get the greedy action(s), for each row in the table, we need only select the action (or actions) corresponding to the column(s) that maximize the row.
### Epsilon-Greedy Policies
-
A policy is
\epsilon
-greedy
with respect to an action-value function estimate
Q
if for every state
s\in\mathcal{S}
,
- with probability 1-\epsilon , the agent selects the greedy action, and
- with probability \epsilon , the agent selects an action uniformly at random from the set of available (non-greedy AND greedy) actions.
### MC Control
- Algorithms designed to solve the control problem determine the optimal policy \pi_* from interaction with the environment.
- The Monte Carlo control method uses alternating rounds of policy evaluation and improvement to recover the optimal policy.
### Exploration vs. Exploitation
- All reinforcement learning agents face the Exploration-Exploitation Dilemma , where they must find a way to balance the drive to behave optimally based on their current knowledge ( exploitation ) and the need to acquire knowledge to attain better judgment ( exploration ).
-
In order for MC control to converge to the optimal policy, the
Greedy in the Limit with Infinite Exploration (GLIE)
conditions must be met:
- every state-action pair s, a (for all s\in\mathcal{S} and a\in\mathcal{A}(s) ) is visited infinitely many times, and
- the policy converges to a policy that is greedy with respect to the action-value function estimate Q .
### Incremental Mean
- (In this concept, we amended the policy evaluation step to update the Q-table after every episode of interaction.)
### Constant-alpha
- (In this concept, we derived the algorithm for constant- \alpha MC control , which uses a constant step-size parameter \alpha .)
- The step-size parameter \alpha must satisfy 0 < \alpha \leq 1 . Higher values of \alpha will result in faster learning, but values of \alpha that are too high can prevent MC control from converging to \pi_* .